The Nov 7 - Nov 13 week woke up late with AtCoder Grand Contest 007 on Saturday (
problems,
results, top 5 on the left,
analysis). The problemset seems quite well-rounded, offering competitors a choice of different strategies. cospleermusora has figured out the winning strategy this time - start with the three hardest problems since they're worth a lot more points, and then solve whichever easy problems there's time for. Great idea and execution!
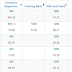
Open Cup 2016-17 Czech Grand Prix took the usual Sunday spot (
results, top 5 on the left). The ITMO 1 team won again and started to create quite a gap at the top of the overall standings. Amazing performance!
Problem J in this round was very easy, and yet it required some thinking to avoid too many special cases in code. You are given an
n times
n grid of uppercase English characters, where
n is at least 3. This grid was built in the following way: first, we fill it with
n different characters in such a way that each row and each column has exactly one occurrence of each character. Then, we replace exactly one character in the entire grid with another character. Your goal is to figure out which character has been replaced, and what was there originally.
In
my previous summary, I've mentioned an interactive Open Cup problem: the judging program has a hidden non-degenerate triangle. The coordinates of its vertices are integers not exceeding 1000 by absolute value. You're allowed to make at most 1000 queries, and your goal is to determine the coordinates of the vertices of the triangle. In each query, you choose a line (more precisely, a half-plane), and you're told the areas of the two parts this line splits the triangle into (one of them can be 0 if it doesn't intersect the triangle).
Here is the solution of our team, which we've created together with Michael Levin: first, we figure out the bounding box of the triangle, using binary search with horizontal and vertical half-planes. At least one of the corners of the bounding box is a vertex of the triangle, which we can find using a 45-degree half-plane which cuts off just one small corner from the bounding box.
When we know a vertex and a 90 degree angle containing the rest, we can use binary search by angle using lines passing through this vertex to find the lines containing the two sides. Finally, we can find the remaining two vertices by binary searching along one of the lines with half-planes parallel to the other line.
This solution has 4 steps, with the first and last step sharing the same binary search problem (given a direction, find the first half-plane with this direction that has non-zero intersection area), so one needed to implement 3 different functions for the interaction. On the good side, the solution doesn't have any special casing at all.
Do you know a simpler approach?
0 komentar:
Post a Comment